Regression

Regression is one of the statistical tools used in the six sigma approach. It lets you know if two variables are related to each other. It determines...

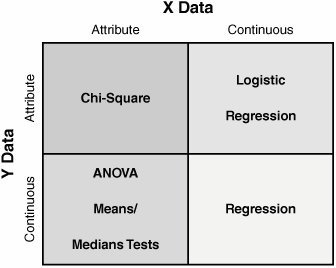
• The statistical significance of a relationship between a Continuous X and a Continuous Y in Y =f(X1,X2,..., Xn).
• The nature of the relationship itself (i.e., the actual equation).

Two Forms:

1) Simple linear, which relates one Continuous Y with one Continuous X

2) Multiple linear, which relates one Continuous Y with more than one Continuous X

For both the simple and multiple techniques, the model parameters are linear in nature, not quadratic or any other power. Given the sheer size of the subject and the application of the tool in Lean Sigma, this page focuses primarily on the simple linear method. For a deeper theoretical understanding, see Introduction to Linear Analysis by Douglas Montgomery and Elizabeth Peck.

Collecting And Analyzing

As with all statistical tests, a sample of reality is required. Generally we require 30 or more data points for the X and the corresponding value of.  This is a passive analysis tool. Do not actively manipulated the process during the data capture. After collecting the requisite number of data you enter the data as two columns into a statistical software package and then analyze it.

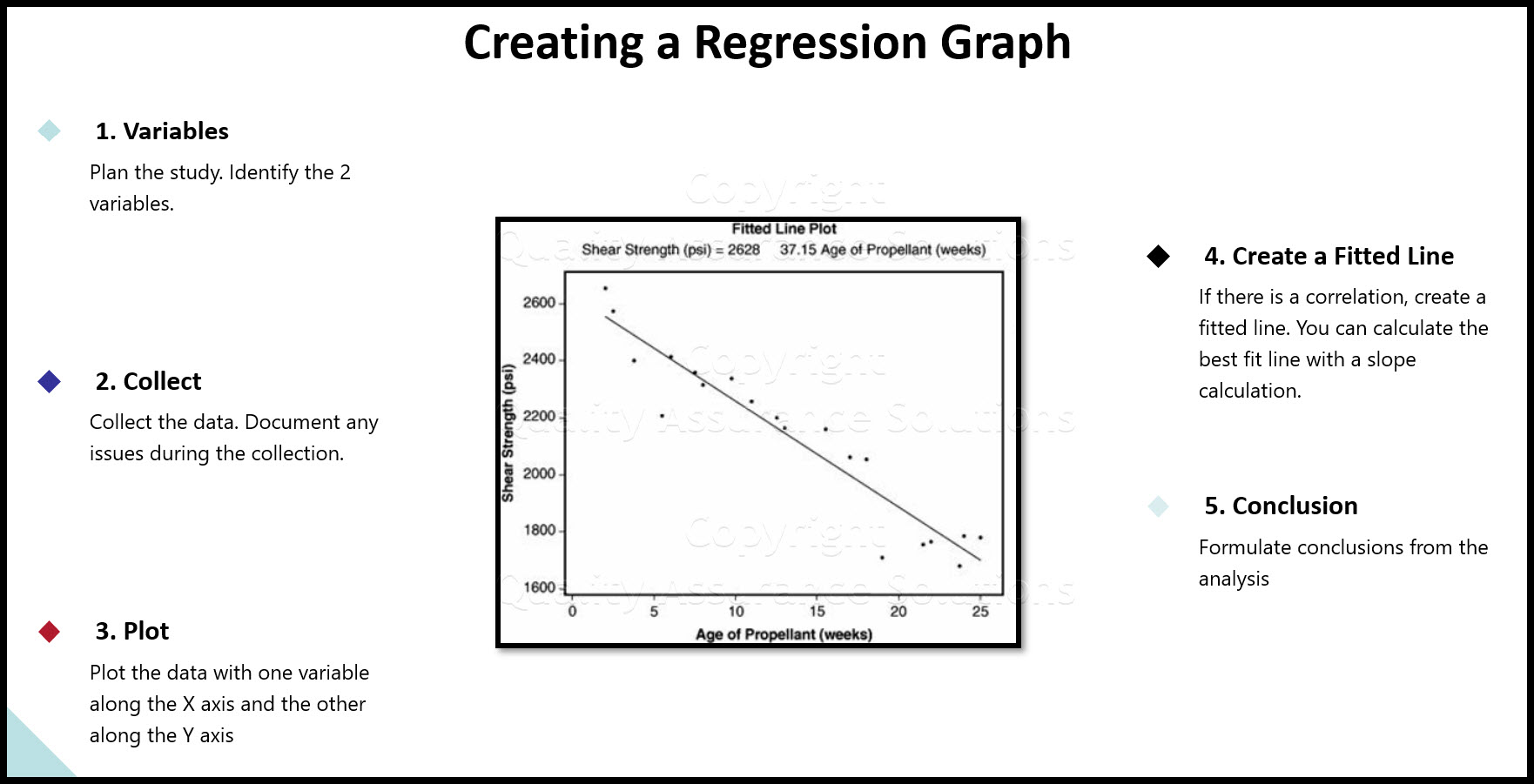
Example Fitted Line Plot

Analyzing the data graphically using a United Plot shows a result similar to the example shown below. Here the X is "Age Of Propellant" in a rocket motor and the Y is "Shear Strength" of the propellant at that age. The data points are plotted on a Scatter Plot. Then a straight line is fitted through them to give the best statistical fit. This is the regression line.

To draw the line we use the least squares method, which minimizes the total squares of all the distances from the line.

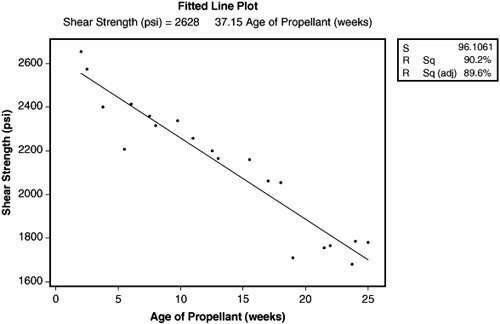
The equation of the regressive straight line (the Regression model) is
 Shear Strength (psi) = 2628 37.15 x Age of Propellant (weeks)

Thus, in the future, for any Age of Propellant from 0 to 25 weeks, it is possible to predict the physical property of Shear Strength. Also, if you need to maintain the Shear Strength above a minimum to perform correctly, then you can calculate a would-be shelf life for the propellant based on the model.

There is no data outside of this time frame and so no predictions should be made beyond 25 weeks.

Roadmap

Problems With Regression

In its simple linear form is quite straight forward to apply. There are, however, as with all tools, several pitfalls that could cause you problems.

This statistic creates a prediction model for behavior of the response Y based on the predictor X. However, if the X itself cannot be predicted, then the model is useless. An example of this might be the desire to predict a electrical power generation maximum daily load from a maximum daily temperature model. But the accuracy of predicting maximum temperature is patchy at best.

Regression is an interpolation technique, not an extrapolation technique. Predictions from regression models are made only with confidence within the confines of the data. If no data has been taken in an operating region, the model is hit and miss at best. To remedy this, take data points over the breadth of the prediction region.

Single points can heavily affect the models. In graph A of the below figure the single outlier dramatically reduces the slope of the model. If the outlier is a bad value, remove the value because the model estimates are wrong and the error is inflated. However, if the outlier is a real process value, it should not be removed. It is a useful piece of data for the process. Refer to notes taken during data collection to understand the point and if possible try to recreate it.

The Effect Of A Single Data Point On The Regression Model

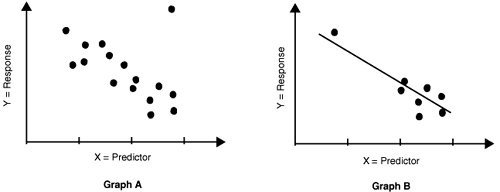
In Graph B the single outlier increases the coefficient. In this case, evaluate the model with and without the point to determine its effect. If the slope value greatly changes during this analysis, then that value is too influential. Conduct other data runs near that point to lower its leverage and confirm its' validity.

Regression models should represent meaningful relationships. Take for example the relationship shown in below figure. Population data within a city correlates with the population density of storks. As much as I'd like to believe this relationship, it could equally be the reverse, mundane scenario. As the town's population increases then there are more chimneys (nesting grounds for storks); thus the stork population increases accordingly.

Incorrect Causal Relationships

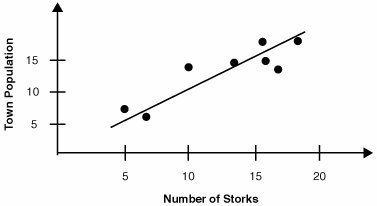
Source SBTI's Lean Sigma Methodology training material